|
Fibonacci RetracementsIn dieser Lesson nehmen wir uns verschiedener Preis-Parameter an, die aus der Fibonacci-Zahlenserie abgeleitet werden. Fibonacci Preiskorrekturen und Fibonacci Preisextensionen stellen die beliebtesten Fibonacci Studien dar. Sie werden benutzt, um Unterstützungs- und Widerstandsniveaus nach signifikanten Auf- oder Abwärtsbewegungen zu bestimmen. Retracements und Extensions bemessen den prozentualen Anteil eines entgegengesetzten Preisschwunges in Relation zur Range des vorangegangenen Preisschwunges. Im weiteren Verlauf soll zunächst dargestellt werden, wie wir aus der Fibonacci Zahlenreihe Prozentwerte („Ratios“) für Support- und Resistance Levels unserer Fibonacci Tools gewinnen. Dabei werden wir zu unseren Gunsten auch Verhältniswerte aufnehmen, die von der einschlägigen Fachliteratur eher vernachlässigt werden. Anhand von praktischen Beispielen soll abschließend die Funktionsweise der Fibonacci Price Retracements und -Extensions demonstriert werden. Welche Prozentwerte sind nun in Betracht zu ziehen? Um diese zentrale Frage zu beantworten, werfen wir einen Blick auf die Fibonacci Zahlenserie, die in der Lesson „Fibonacci Time Counts“ beschrieben wurde. Fibonacci ZahlenserieDie Entdeckung dieser Zahlenreihe wird Leonardo Fibonacci da Pisa (1170 - 1240) zugesprochen. In seinem berühmten Werk „Liber Abacci“ schilderte Fibonacci die folgende Untersuchung einer angenommenen Kaninchenpopulation: Ein Kaninchenpaar wird in einem abgeschlossenen Gebiet ausgesetzt. Untersucht werden sollte, wieviele neue Kaninchenpaare nach einem Jahr das abgeschlossene Gebiet bevölkern. Dies unter der Annahmen, dass jedes neu geborene Kaninchenpaar nach einem Monat zeugungsfähig wäre und nach einem weiteren Monat ein neues Kaninchenpaar hervorbringen würde. Todesfälle wurden ausgeschlossen. Fibonacci ging nach einem Monat Tragzeit bei jedem Wurf von zwei Jungen aus, einem männlichen und einem weiblichen, siehe Abbildung 1.
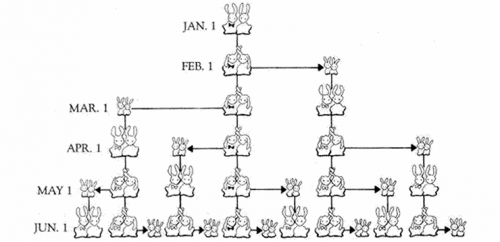
Die Zahl der Kaninchenpaare bleibt in den ersten beiden Monaten konstant auf 1, weil jedes Paar (einschließlich des ersten Paares) einen Monat benötigt, um zeugungsfähig zu werden und um dann jeden Monat ein neues Paar hervorzubringen. Das erste Kaninchenpaar erzeugt während des zweiten Monats ein neues Paar, so dass zu Beginn des dritten Monats zwei Paare existieren. Von diesen bringt das ältere Paar ein drittes hervor. Damit erweitert sich die Zahlenfolge auf 1, 1, 2, 3. Die Summe zweier benachbarter Zahlen ergibt in dieser Zahlenfolge jeweils die nächsthöhere Zahl, wie folgendes Beispiel zeigt:
Erstes Zahlenpaar (beginnend) mit 1: 1, 2 Summe aus dem Zahlenpaar: 1 + 2 = 3 Zahlenfolge: 1, 1, 2, 3 Summe des letzten Zahlenpaares: 2 + 3 = 5 Neue Zahlenfolge: 1, 1, 2, 3, 5 Summe des letzten Zahlenpaares: 3 + 5 = 8 Neue Zahlenfolge: 1, 1, 2, 3, 5, 8 usw.
Nach einem Zeitraum von nur zehn Monaten erhält man eine Anzahl von 354,224,848,179,261,915,075 Kaninchenpaaren. Das Pikante an dieser Zahlenfolge ist nicht das absolute Ergebnis, sondern die Verhältnismässigkeit, welche die Zahlen untereinander aufweisen. Betrachten wir einmal die Zahlen der Fibonacci Zahlenserie: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 134, 233, 377, 610..... Mit Hilfe dieser Zahlenfolge lässt sich die irrationale Zahl PHI (ϕ) ermitteln, auf deren Grundlage die Berechnung von Retracements und Extensions erfolgt. Der Wert von ϕ beträgt ≈1,618. Diese Relation erhalten wir, wenn wir eine Zahl aus der Folge durch die vorhergehende Zahl, z.B. 55 : 34 oder 89 : 55 dividieren. Die daraus resultierende Zahlenfolge nähert sich asymptotisch einer konstanten Relation, welche 1,61803398875 lautet und eine irrationale Zahl ist. Wenn wir jede Zahl der Fibonacci Zahlenserie durch die nachfolgende Zahl dividieren, also eine reziproke Berechnung durchführen, z.B. 34 : 55 oder 55 : 89, erhalten wir die Relation PHI‘ mit ϕ‘ ≈ 0,618, wobei es sich lediglich um den Kehrwert von PHI handelt. Mit der Entdeckung der Zahlenserie leitete Fibonacci die Abkehr vom umständlichen römischen Zahlensystem und die Einführung des Dezimalsystems in der europäischen Mathematik ein. Fibonacci Ratios Mit ϕ ≈ 1,618 und ϕ‘ ≈ 0,618 haben wir schon erste Ratios für eine Extension beziehungsweise ein Retracement erhalten. Wir drücken die beiden Ratios als Prozentwerte aus: 61,8% und 161,8%. Nun machen wir uns daran, weitere Ratios aus der Fibonacci Zahlenserie abzuleiten. Wurden bei ϕ ≈ 1,618 beziehungsweise ϕ‘ ≈ 0,618 noch benachbarte Zahlenwerte der Fibonacci Zahlenserie dividiert, so dividieren wir im folgenden eine Zahl durch die vorletzte beziehungsweise vor-vorletzte Zahl der Fibonacci Zahlenfolge. Rechnerisch sähe das dann beispielsweise so aus: Vorletzte Zahl 89 : 34 = 2,618 bzw. 261,8% Reziproke Berechnung 34 : 89 = 0,382 bzw. 38,2% Vorvorletzte Zahl 55 : 13 = 4,236 bzw. 423,6% Reziproke Berechnung 13 : 55 = 0,236 bzw. 23,6% Wenn Sie diese Art von Rechnungen mit anderen Zahlen aus der Fibonacci Zahlenserie praktisch nachvollziehen, wird Ihnen auffallen, dass die Ratios umso genauer werden, je höher die beiden Zahlen gegen unendlich laufen. Interessant sind in diesem Zusammenhang auch folgende beispielhafte mathematische Beziehungen der Fibonacci Relationen untereinander (wichtige Herleitungen in Fettschrift): 0,236 = 1 : 4,236 0,382 = 1 – 0,618 0,382 = 0,618 x 0,618 0,382 = 0,618 : 1,618 0,382 = 1 : 2,618 0,618 = 1 : 1,618 0,618 = 0,382 x 1,618 1,618 = 2,618 x 0,618 1,618 = 1 x 1,618 2,618 = 1,618 x 1,618 4,236 = 2,618 x 1,618 Wir fügen nun den bisher ermittelten Fibonacci Relationen noch 1,000, deren Transformation 0, 500 und 2,000 (Wurzel aus 4 als harmonisches Ratio, im Sinne einer Extension auch als „Measured Move“ bekannt) hinzu und erhalten für Retracements und Extensions folgende Ratios: Mehrwert durch vernachlässigte Fibonacci Retracements Fibonacci Ratios, die in der Fachliteratur und auf den Märkten vernachlässigt werden, weil sie der Elliott Wave-Theorie nicht anhaften, lau- Fortsetzung – Know How – Fibonacci Retracements ten 78,6% und 127,2%. 1,272 ist die Wurzel aus ϕ ≈ 1,618 und 78,6 ist der Kehrwert von 1,272 (1 : 1,272). Beide Verhältniswerte sind geometrische Ratios. Die Hinzunahme dieser Ratios kann einen entscheidenden Analyseund Handelsvorteil generieren, insbesondere wenn es um spezielle Analyse-/Handelsmethoden geht, auf die ich in noch folgenden Lessons eingehen werde. Damit steht unsere Liste der wichtigsten Fibonacci Ratios endgültig fest. Sie lauten wie folgt:
Retracements 23,6% 38,2% 50% 61,8% 78,6% 100%
Extensions 127,2% 161,8% 200% 261,8% 423,6%
Von diesen Ratios werden 23,6%, 200%, 261,8% und 423,6% eher seltener gebraucht. Nichtsdestotrotz sollten Sie auch diese Prozentsätze in ihren Charts „plotten“. Soviel einstweilen zu diesen Zahlen, die bei professionellen Börsenhändlern sehr beliebt sind und weithin verwendet werden, um das Ausmaß einer Korrektur zu bemessen und dementsprechend Indikationen für ihre Handelsaktivitäten zu erhalten. Fibonacci Levels - Support und ResistanceNachdem wir uns bis jetzt etwas ausführlicher mit den mathematischen Verhältnismäßigkeiten der Fibonacci Zahlenserie beschäftigt haben, betrachten wir im Folgenden die Funktionseigenschaften von Fibonacci Price Retracements und –Extensions. Fibonacci Price Retracements Fibonacci Price Retracements weisen auf potentielle Unterstützungs- beziehungsweise Widerstands-Levels hin. Für das Antragen der Retracements im Rahmen einer Aufwärtskonstruktion wird zunächst der Tiefpunkt (100% Retracement) mit dem nachfolgenden Hochpunkt (0% Retracement) verbunden. Entsprechend der Kursdifferenz dieser beiden Extrempunkte werden dann vom Hochpunkt ausgehend die Retracements in Prozenten (23,6%, 38,2%, 50%, 61,8% und 78,6%) gemessen und als horizontale Linie von der Charting Software eingezeichnet, siehe folgende Abbildungen. Retracements 23,6% 38,2% 50% 61,8% 100%
Extensions 161,8% 200% 261,8% 423,6%
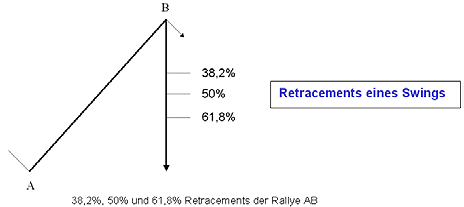

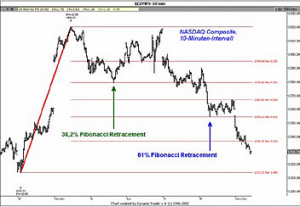
Sie erkennen auf Anhieb, dass ein „Retracement“, welches 100% überschreitet zu einer „Extension“ wird. Übertragen auf den Markt heisst das: Wenn die Range eines vorangegangenen Preisschwungs nur korrigiert wird, handelt es sich um Retracement. Wird diese Range hingegen überschritten („extensiert“), handelt es sich um eine Extension. Im Chart sehen Sie den NASDAQ Composite (COMP) in einem 10-Minuten-Intervall. Vom Beginn des Aufwärtsschwunges vom 01. November 2002 (10 Uhr) bis zum Schwunghoch am 04. November 2002 (12:30 Uhr) projizieren wir mit der Charting Software die Retracements. Sie erkennen, wie das 38,2% Retracement als Unterstützung fungiert, von welcher aus der Index eine größere Aufwärtskorrektur startete. Im weiteren Verlauf dient in diesem Beispiel das 61,8% Retracement als leichte kurzfristige Unterstützung, die aber dann schließlich unterboten wird. Die meisten Elliott Wave-Theoretiker lehren, dass das 61,8% Retracement die kritische Zone ist, welche signalisiert, ob ein aktueller Swing ein Counter-Trend Swing ist oder hingegen ein Swing in eine neue Trendrichtung. Mit anderen Worten: Ihrer Meinung nach sollten Counter-Trends oder Korrekturen das 61,8% Retracement nicht überschreiten. Wenn das 61,8% Retracement aber überschritten werden sollte, wird angenommen, dass der Markt eine neue Trendrichtung eingeschlagen hat und kein Counter-Trend ist. Dem muss man entgegnen, dass das 61,8% Retracement zwar einen wichtigen potentiellen Support oder Resistance darstellt, aber nicht immer als Trendsignal bezeichnet werden kann. Denken Sie nur an eine Welle 2, die oft an einem 78,6% Retracement endet bevor die meist dynamische Welle 3 startet. Aus diesem Grund ist auch eine 78,6% Preiskorrektur ein wichtiges Retracement Level, das gewöhnlicherweise nicht unterschritten werden sollte, wenn die vorangegangene Trendrichtung fortgesetzt wird. Natürlich können Sie die Retracements auch in höheren Intervallen als im vorigen Beispiel des 10-Minuten-Intervalls einsetzen. Und: Sie können natürlich auch – wie zuvor erwähnt – Retracements zur Lokalisierung potentieller Widerstände einer Aufwärtskorrektur einsetzen. Die Vorgehensweise bei der Erstellung einer solchen Retracement-Konstruktion ist die gleiche, wobei hier natürlich die Retracements vom Tiefpunkt ausgehend abgezählt werden, das heißt innerhalb der beiden Extrempunkte liegt unten das 23,6%-Retracement und oben das 76,8% Retracement. In der folgenden Abbildung 5 sehen Sie ein Chart des S&P 500 Index (SPX) in einem Wochen-Intervall.
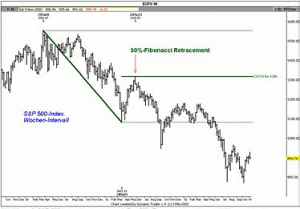
Im Chart sehen Sie, wie das 50% Retracement des Abwärtsschwunges vom 25.03.2000 bis zum 24.03.2001 einen Widerstand markiert, welcher das Ende dieser Bärenmarkt-Rallye am 26.05.2001 bedeutet. Bleiben wir beim S&P 500 Index im Wochen- Intervall. Nachdem die Rallye - wie vorhin beschrieben - in der Woche des 26.05.2001 am 50% Retracement endete, crashte der Markt und bildete in der Woche des 22.09.2001 ein neues Low. Von diesem Tief startete eine weitere Rallye. Nun könnten wir beispielsweise wie folgt vorgehen: Wir benutzen das Hoch in der Woche des 26.05.2001, in der unsere Rallye vorhin am 50% Retracement endete, als Schwunghoch und das Tief in der Woche des 22.09.2001 als Schwungtief und projizieren von diesem Swing abermals die Retracement Levels, siehe Abbildung 6.
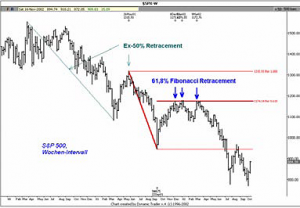
Im Chart sehen Sie unser ehemaliges 50% Retracement unseres in der Abbildung 5 beschriebenen Preisschwungs (beides in türkiser Farbe). Das Schwunghoch an diesem 50% Retracement bildet mit dem Low in der Woche des 22.09.2001 wieder einen anderen Swing, von dem wir unsere Retracements abermals projizieren können (rot). Sie sehen, dass auch diese Bärenmarktrallye an einem Fibonacci Retracement endete: Der Markt schaffte es nämlich in mehreren Anläufen nicht, das 61,8% Retracement Level zu überwinden (Woche des 8.12.2001, 05.01.2002, 09.03.2002). Merken Sie sich: Ein Markt, der weniger als 100% des vorangegangenen Swings korrigiert, ist immer ein Counter- Trend-Swing oder anders formuliert eine Korrektur des vorangegangenen Swings. Frank Thönnißen
Dieser Artikel stammt aus dem TradersJournal 16/09 |
|

